
Il y a encore quelques années, si je voulais créer des images numériques hyperréalistes, il me fallait des compétences pointues en modélisation 3D, en rendu physique ou des heures de travail acharné sur Photoshop. Aujourd’hui, il me suffit de taper une phrase, un simple « prompt » : « génère moi une image réaliste de l’homme du lapin (soit fidèle à la source) qui roulent dans un décapotable verte dans le désert du Nevada, le xénomorphe (du film alien) fait du stop sur le bord de la route sur le dos d’une licorne arc en ciel ». Quelques secondes plus tard, je vois l’image apparaître, non pas extraite d’une immense base de données secrète, mais générée de toutes pièces, pixel par pixel. Plus récemment encore, j’ai vu cette prouesse s’étendre à la vidéo, ajoutant une dimension temporelle vertigineuse à cette création ex nihilo.
Pendant longtemps, le monde de l’IA générative visuelle que j’observais était dominé par les GANs (Réseaux Antagonistes Génératifs). Bien que puissants, ils étaient notoirement instables et peinaient à générer des images très complexes à partir de textes précis. Puis, une révolution silencieuse a eu lieu au croisement de l’apprentissage profond (deep learning) et de la physique thermodynamique.
Face à ces résultats stupéfiants, je suis souvent tenté de crier à la magie. Pourtant, sous le capot de ces modèles génératifs de pointe, se cache une mécanique d’une élégance mathématique rare. J’ai voulu comprendre comment ces modèles fonctionnent réellement, et cela demande de dépasser les explications superficielles du type « l’IA a regardé beaucoup d’images ». C’est en fait un processus complexe de sculpture du bruit, guidé par une compréhension mathématique et sémantique du langage humain.
Dans cet article, je vais déconstruire pour vous cette mécanique en trois étapes fondamentales : la création d’un langage commun entre la machine et l’image, la structuration de la matière à partir du chaos absolu, et enfin, l’astuce mathématique cruciale qui permet à l’IA de suivre nos instructions à la lettre.
Partie 1 : La Pierre de Rosette Numérique (Comprendre le lien Texte-Image)
Avant qu’une IA puisse me « dessiner » un chat, elle doit comprendre fondamentalement ce qu’est un « chat », et comment ce concept purement linguistique se traduit visuellement. Si je montre une image de chat à un ordinateur, il ne voit qu’une grille de nombres. Comment faire le pont entre ces pixels froids et le mot « chat » ?
La réponse que j’ai découverte réside dans ce qu’on appelle les espaces latents et une technique d’apprentissage révolutionnaire nommée l’apprentissage contrastif, popularisée notamment par l’architecture CLIP (Contrastive Language-Image Pre-training).
1.1 La magie des espaces vectoriels à haute dimension
Pour comprendre CLIP, il m’a fallu d’abord saisir comment l’IA lit le texte. Les algorithmes modernes ne lisent pas les lettres, ils placent des mots dans un espace géométrique. J’imagine un espace gigantesque, non pas en 3 dimensions, mais possédant des centaines, voire des milliers de dimensions. Dans cet espace, chaque mot, chaque concept est un « point » défini par un vecteur (une longue liste de coordonnées).
L’idée est que des mots ayant un sens similaire seront placés proches l’un de l’autre dans cet espace. « Chien » sera géométriquement proche de « Chiot » et de « Loup », mais très loin de « Gratte-ciel ». Plus fascinant encore, cet espace permet des mathématiques sémantiques : si je prends les coordonnées du mot « Roi », que j’y soustrais les coordonnées de « Homme » et ajoute celles de « Femme », j’atterris exactement sur les coordonnées du mot « Reine ».
Le coup de génie de CLIP a été d’étendre ce concept au monde visuel. L’objectif ? Créer un espace vectoriel unique où les images et les textes qui les décrivent « habitent » exactement au même endroit.
Pour ce faire, le système utilise deux réseaux de neurones distincts fonctionnant en tandem :
- Un encodeur d’images : Il prend une image de pixels et la compresse pour la transformer en un vecteur de 512 dimensions.
- Un encodeur de texte : Il prend une phrase et fait exactement la même chose, produisant un autre vecteur de 512 dimensions.
1.2 Le jeu des paires contrastives
Au début de l’entraînement, ces encodeurs sont « stupides ». Le vecteur d’une image de chien peut se retrouver à l’autre bout de l’espace latent par rapport au vecteur de la phrase « une photo de chien ». C’est là qu’intervient l’apprentissage contrastif.
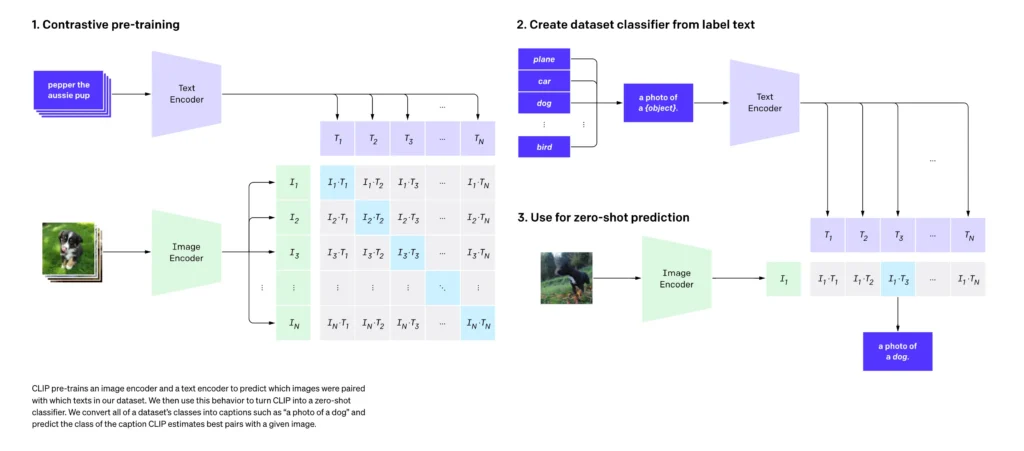
On nourrit le modèle avec des centaines de millions de paires (image, texte descriptif) aspirées sur Internet. J’imagine cela comme une matrice géante. Sur les lignes, j’ai les descriptions textuelles d’un lot d’images. Sur les colonnes, les images correspondantes.
L’objectif de l’entraînement est d’optimiser le modèle pour :
- Maximiser la similarité entre les paires correspondantes (la diagonale de ma matrice). Géométriquement, l’IA force l’encodeur d’image et l’encodeur de texte à orienter leurs vecteurs respectifs dans la même direction exacte.
- Minimiser la similarité entre toutes les autres paires. L’IA repousse activement le vecteur de l’image « chat » loin du vecteur du texte « voiture rouge ».
C’est cette fondation, cette véritable Pierre de Rosette numérique, qui permet à l’IA de « comprendre » mes prompts. Cependant, comprendre un texte n’est pas dessiner. CLIP est un critique d’art exceptionnel, mais c’est un piètre peintre. Pour générer l’image, il me faut un autre moteur.
Partie 2 : Sculpter le Chaos (Les Modèles de Diffusion)
La véritable révolution visuelle de la décennie est née de l’adoption des Modèles Probabilistes de Diffusion (DDPM). L’idée centrale m’a paru profondément contre-intuitive au début : pour apprendre à créer la beauté et la structure, l’intelligence artificielle doit d’abord apprendre à les détruire systématiquement.
2.1 Le processus aller : La thermodynamique de la destruction
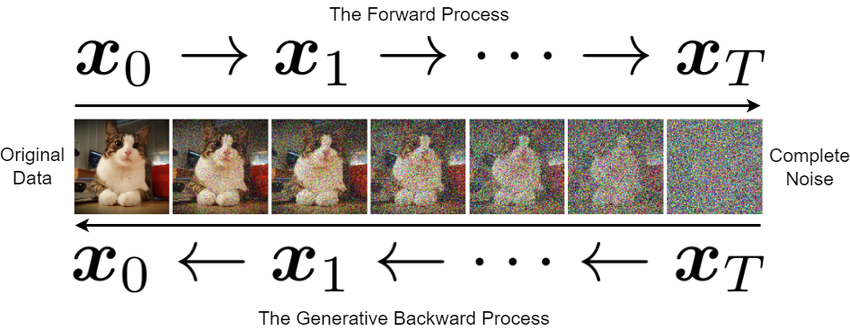
Le principe s’inspire directement de la physique statistique (le mouvement brownien). Imaginons le processus d’entraînement. Je prends une image parfaitement nette de notre ensemble de données. Le processus de diffusion « aller » (forward process) consiste à détruire cette information en y ajoutant progressivement du bruit gaussien (une sorte de neige télévisuelle).
- Étape 0 : Image originale, parfaitement claire.
- Étape 500 : Les formes commencent à se dissoudre sévèrement dans la neige statique.
- Étape 1000 : L’image originale a totalement et irrémédiablement disparu. Il ne reste qu’un carré de bruit aléatoire absolu.
Ce processus est mathématiquement défini et fixe. J’ai transformé une donnée hautement structurée en un chaos parfait.
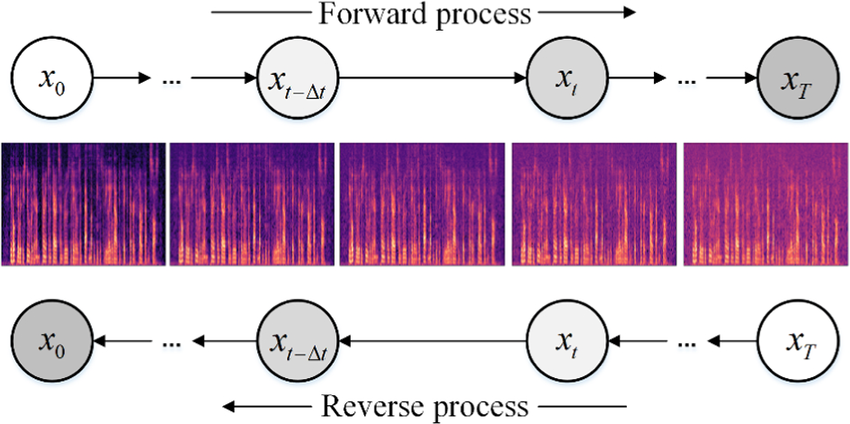

STOCHASTIC DIFFERENTIAL EQUATIONS
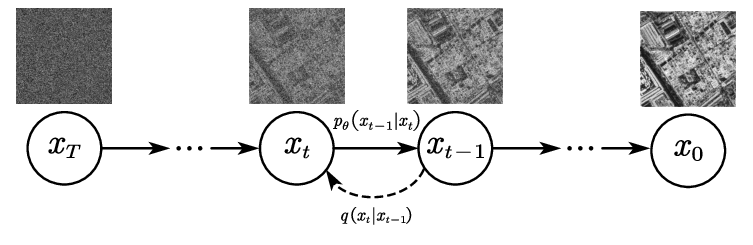
2.2 Le processus retour : La genèse à rebours
Le coup de génie des chercheurs a été d’entraîner un immense réseau de neurones (souvent une architecture U-Net) à inverser l’entropie de ce processus temporel.
L’entraînement se déroule ainsi : je donne au réseau de neurones l’image bruitée à une étape aléatoire (par exemple l’étape 450). Je lui donne aussi cette valeur temporelle pour qu’il sache « à quel point » l’image est censée être détruite. Sa mission est de deviner : « Parmi tout ce bruit que tu vois, quelle est la part exacte de bruit qui vient d’être ajoutée ? »
Plutôt que d’essayer de deviner l’image finale d’un coup sec, le réseau apprend à modéliser le vecteur de bruit pour le soustraire mathématiquement et retrouver l’image de l’étape 449, un peu plus nette.
2.3 Le paradoxe de la moyenne : Pourquoi l’IA réinjecte-t-elle du bruit ?
C’est l’une des caractéristiques que je trouve les plus fascinantes. Lors de la génération d’une nouvelle image, je pars de l’étape 1000 avec du pur bruit. Je demande au réseau de prédire le bruit, je le soustrais, et ainsi de suite. Logiquement, je devrais simplement « nettoyer » l’image pas à pas.
Pourtant, dans l’algorithme original, après avoir soustrait le bruit prédit, l’algorithme rajoute délibérément une petite dose de nouveau bruit aléatoire avant de passer à l’étape suivante. Pourquoi saboter son propre travail ?
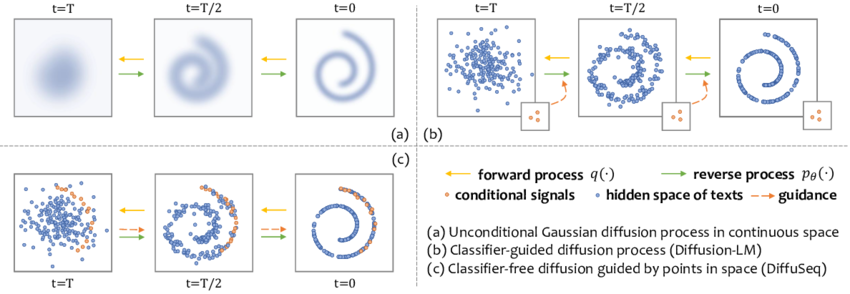
Pour le comprendre, il faut s’imaginer l’espace de toutes les images possibles. Les images « réelles » et cohérentes occupent un espace extrêmement restreint, comme une fine ligne sinueuse, une spirale complexe.
Quand le modèle regarde un point très bruité (très loin de la spirale), son objectif est de pointer vers elle. Mais au début, le bruit pur est à égale distance de toutes les images possibles. Le réseau a tendance à pointer vers la moyenne de toutes les images possibles de son set d’entraînement (une bouillie grisâtre et floue).
Si je me contente de suivre la prédiction de manière purement déterministe, j’obtiendrai une image sans détails. En rajoutant du bruit à chaque étape, je force le point à « trembler » pendant qu’il se dirige vers la spirale. Cette agitation l’empêche de s’échouer sur la moyenne et lui permet de « tomber » sur une branche spécifique, nette et détaillée.
Partie 3 : Prendre le Contrôle (Conditionnement et Guidage CFG)
J’ai maintenant deux pièces maîtresses isolées : CLIP (qui comprend le texte) et le U-Net de Diffusion (qui sculpte l’image). Le but est de les fusionner. Comment dire au moteur de diffusion quelle partie de la spirale il doit viser ?
3.1 Le conditionnement : Murmurer à l’oreille du bruit
Lorsque je valide mon prompt, le texte passe d’abord dans l’encodeur de texte de CLIP, qui recrache un vecteur dense de coordonnées sémantiques. Ce vecteur est injecté directement dans les entrailles du réseau de diffusion (via l’Attention Croisée).
Au lieu de se demander « Comment rendre cette bouillie de pixels plus réaliste ? », le réseau se demande « Comment la rendre réaliste, sachant que cela doit finir par ressembler au concept d’un astronaute ? ».
3.2 Le secret de l’obéissance aveugle : Le « Classifier-Free Guidance » (CFG)
Cependant, dans la pratique, j’ai souvent remarqué qu’un simple conditionnement ne suffisait pas. Si je demandais « un astronaute tenant une pomme verte sur la lune », le modèle générait souvent juste un astronaute générique.
C’est là qu’est née l’astuce la plus importante : le Guidage sans classifieur (Classifier-Free Guidance ou CFG). C’est ce fameux paramètre « Guidance Scale » que l’on manipule dans les interfaces.
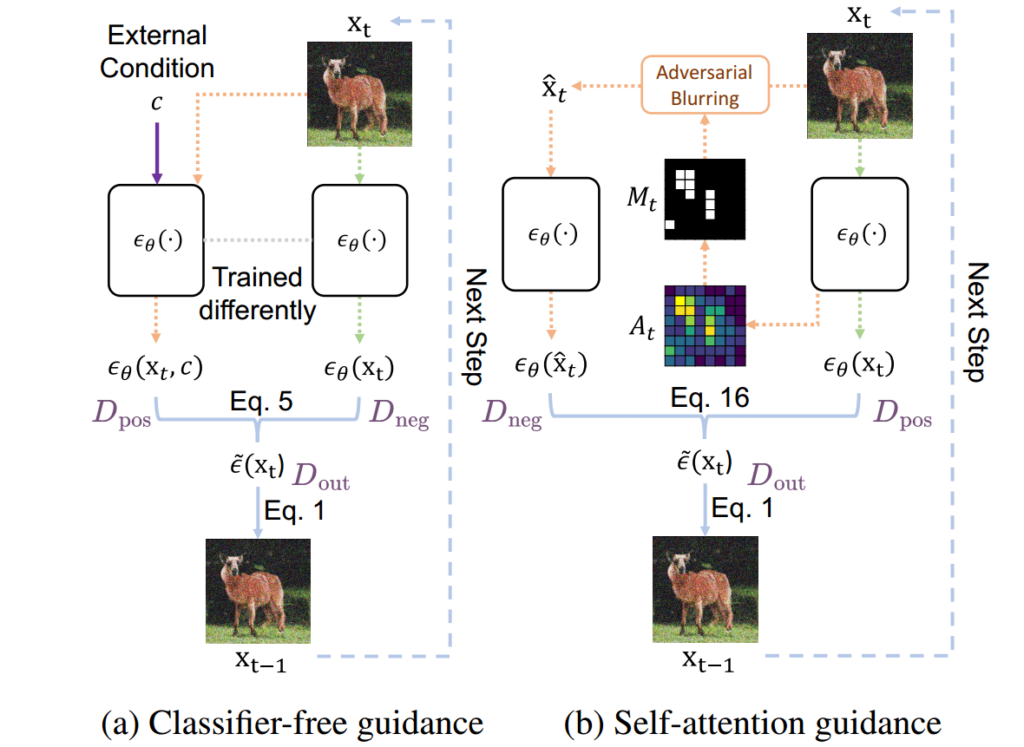
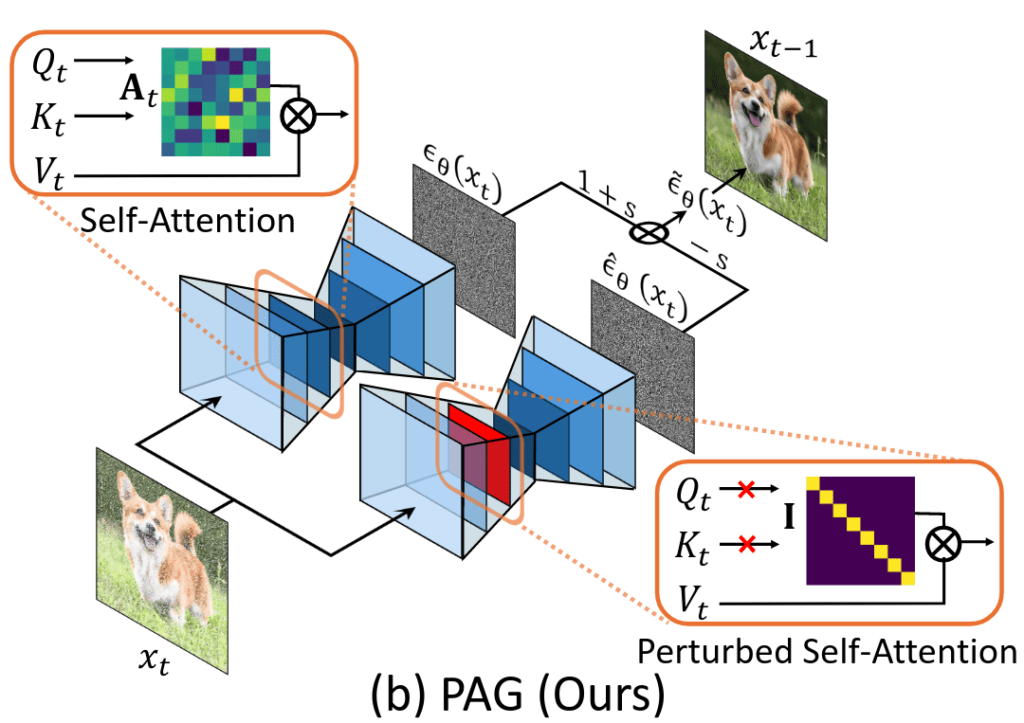
L’idée du CFG est de forcer mathématiquement le modèle à être radical dans son adhésion à mon texte. Voici comment cette magie opère :
- La passe silencieuse : Le modèle regarde l’image bruitée, et on lui cache mon prompt. Il génère un vecteur prédisant la direction pour rendre l’image simplement « réaliste ».
- La passe attentive : Le modèle regarde la même image, mais cette fois en lisant mon prompt. Il génère une nouvelle direction de débruitage conditionnée.
- L’extraction de l’essence pure : On soustrait le vecteur générique du vecteur conditionné. Cette soustraction isole l’essence pure de mon prompt.
- L’amplification : On multiplie ce vecteur d’essence pure par le facteur d’échelle CFG et on l’ajoute à la prédiction inconditionnelle.
En langage courant, voici ce que je dis au réseau via le CFG : « Je vois où tu irais naturellement. Je vois aussi où tu irais avec mon texte. Calcule la différence, multiplie cette urgence par 8, et fonce dans cette direction en ignorant tes instincts de base ! »
3.3 L’ingénierie inversée des défauts : Les Prompts Négatifs
Le corollaire magnifique du CFG, ce sont les « prompts négatifs ». Si je tape « flou, mauvaise anatomie, doigts supplémentaires », le système calcule le vecteur vers ces mots horribles et le soustrait activement de la trajectoire finale. Le processus est mathématiquement repoussé loin des zones contenant des mains à six doigts.
Conclusion : La grammaire de la nouvelle réalité
Pour moi, la génération d’images et de vidéos par IA n’est pas un banal tour de passe-passe. C’est le triomphe absolu de la modélisation mathématique des espaces à très haute dimension.
En combinant l’apprentissage de la sémantique humaine avec la puissante modélisation des probabilités thermiques inversées, et en y appliquant une algèbre vectorielle agressive pour forcer l’obéissance, nous avons créé un nouveau paradigme de création. J’utilise aujourd’hui mes mots comme des scalpels pour sculpter le bruit probabiliste.
La prochaine fois que je taperai un prompt et que je verrai une image époustouflante émerger du néant en quelques secondes, je prendrai un instant pour imaginer cette tempête de bruit mathématique, repoussée et modelée en arrière dans le temps, guidée par la force gravitationnelle de mes mots. Ce n’est pas de la magie, et c’est précisément pour cela que c’est si fascinant.
Sources et références scientifiques
Pour la rédaction de cet article et pour celles et ceux qui souhaitent creuser les fondations mathématiques de ces technologies, je me suis appuyé sur les travaux de recherche fondateurs suivants :
Sur l’alignement Texte-Image (CLIP) :
- Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., … & Sutskever, I. (2021). Learning Transferable Visual Models From Natural Language Supervision. OpenAI. Lien : https://arxiv.org/abs/2103.00020
Sur la création des Modèles de Diffusion (DDPM) :
- Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. (2015). Deep Unsupervised Learning using Nonequilibrium Thermodynamics. Stanford University / UC Berkeley. Lien : https://arxiv.org/abs/1503.03585
- Ho, J., Jain, A., & Abbeel, P. (2020). Denoising Diffusion Probabilistic Models. UC Berkeley. Lien : https://arxiv.org/abs/2006.11239
Sur l’accélération du processus (DDIM) :
- Song, J., Meng, C., & Ermon, S. (2021). Denoising Diffusion Implicit Models. Stanford University. Lien : https://arxiv.org/abs/2010.02502
Sur le contrôle de l’IA (Classifier-Free Guidance) :
- Ho, J., & Salimans, T. (2021). Classifier-Free Diffusion Guidance. Google Brain. Lien : https://arxiv.org/abs/2207.12598